【ベストコレクション】 ��の数の平方根 高校 298274-��の数の平方根 高校

ルートの中が 負の数の２乗 のときの ルートのはずし方 数学 苦手解決q A 進研ゼミ高校講座

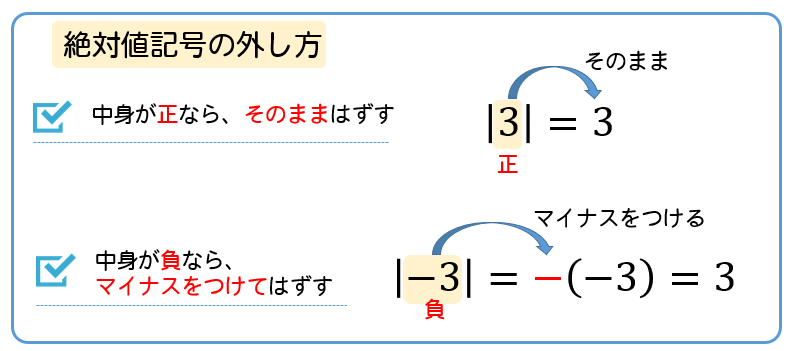
 そして，負の数の平方根は存在しないとしていること． だから公式として √a x √b = √ (ab) を出すときには，a>0,b>0がついている なお，aまたはbが0のケースは0の平方根は0しか存在せず 0の平方根を√0と表し，0=√0であるというような意味の 言明があるはず． 重要なのは，表記のルールを設定する際に その表記が適用可能な前提条件を明確にするという 当たり前のこと． なお，負の数を表すときはマイナスをつける。 − 4 = −2 この根号を使うと平方根が整数にならないような場合でも平方根を表すことができる。 例 16の平方根は± 16 =±4 2の平方根は± 2 15の平方根は± 15 xの平方根は± x 負の数には平方根が存在しないので 根号の中は必ず正の数 である。 上の例で言うとxは必ず正でなければならない。 a 2 の平方根 ( ) 2 = A のとき に入る数をAの平方根という すると

負の数の平方根 高校

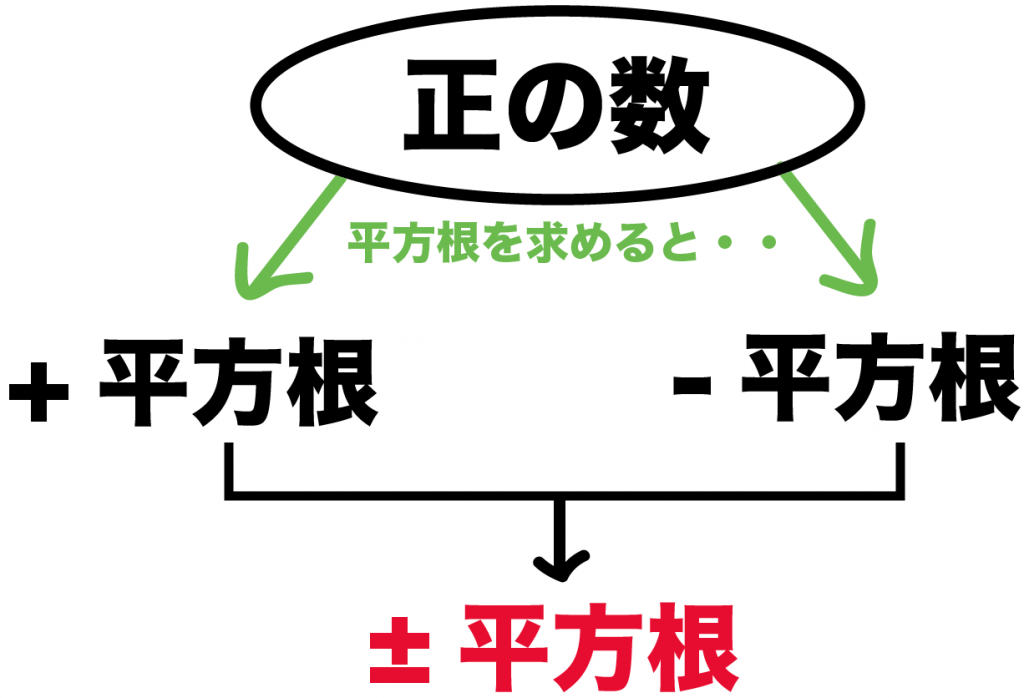
負の数の平方根 高校-負の数のn乗根！ an a n や n√a a n について、 今まではずーっと a > 0 a > 0 で話を進めてきました。 え？ そうだったけ？ って人も多いと思います。 a a が正なのか負なのか、特別気にしていなかったという人が多いと思います。 別にそれでOKです。 まずは出題された計算が正確にできるようになることが最重要事項だからです。 そして、 a a が負の数で出題されることなんて（まず）ないからでつまり， の平方根は， にあてはまる の値のことです。 《例》 16 の平方根は，正の数では 4，負の数では－ 4 です。 ( 4 より 4,4 ) ☆正の数の平方根は，正の数と負の数の 2 つあって，その絶対値は等しくなります。 ☆ 0 の平方根は 0 です。

全て分かりません 1個でもていいので教えて頂きたいです Clearnote

 無料の数学プリント～平方根～ 学びの森 中学生必見！ 無料の数学プリント～平方根～ 「2乗して2になる数は？ 」という問題に対して、それを解決してくれるのが平方根です。 小学校では自然数から小数、分数と学習し、中学1年では負の数が導入され そのほかの回答（1件） @genzi_hikaru 21/3/22 214 √nは、2乗してnになる数のうち正の数を表します。 例えば2^2=4より√4=2です。 区別してほしいものとして「平方根」があります。 nの平方根は2乗してnになる数（負でも良い）を表します。 例えば√4=±2ですAの平方根 は 方程式 a=b^2 の解b で±√a つまり2つあります。 √ (根号)は正の平方根を現す記号です。 #複素数が絡むとさらにややこしくなりますが・・・ 0 件 通報する No4 回答者： kairou 回答日時： 1505 「√6の負の平方根」と云う言葉は、何処に書いてあったのですか。 多くの人が勘違いしてますが、√6＞0 です。 負に

 数学 高校数学 平方根 の定義 平方根 ：2乗するとaになる数、すなわち x 2 =a となるxをaの 平方根 といいます。 √a ：aの 正の 平方根 （ルートaと読みます） √a ：aの負の 平方根 ここで注意してほしいのは「 平方根 ≠ルート 」ということです。 平方根 のうち正のものを「ルート〇」と呼ぶ んです。 これが間違えやすく重要なので気を付けましょう。 また 、√0＝0 と定めます。 厳 0の平方根は0だけになります。 ＊負の数の平方根は存在しません。 3の平方根 ←なしと答えましょう。（高校数学では3の平方根で虚数というものを習います。） 間違えやすい問題 36の平方根は6である ←間違いになります。高校数学 >> 高校数学Ⅰ・A >> 数と式 現在地 と前後の項目 対称式の変形 / 実数と根号（公式と例） / 根号計算1 / 根号計算2 / 分母の有理化 / 無理数の独立 / 式の値 (無理数の対称式) / x n 1/x n の値 / センター試験問題 平方根の計算 / 根号計算の入試問題

負の数の平方根 高校のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

おとな数学塾 Home Facebook	おとな数学塾 Home Facebook	おとな数学塾 Home Facebook
おとな数学塾 Home Facebook	おとな数学塾 Home Facebook	おとな数学塾 Home Facebook
おとな数学塾 Home Facebook	おとな数学塾 Home Facebook	おとな数学塾 Home Facebook
おとな数学塾 Home Facebook	おとな数学塾 Home Facebook	おとな数学塾 Home Facebook
おとな数学塾 Home Facebook	おとな数学塾 Home Facebook	おとな数学塾 Home Facebook
おとな数学塾 Home Facebook	おとな数学塾 Home Facebook	おとな数学塾 Home Facebook
おとな数学塾 Home Facebook	おとな数学塾 Home Facebook	おとな数学塾 Home Facebook
おとな数学塾 Home Facebook	おとな数学塾 Home Facebook	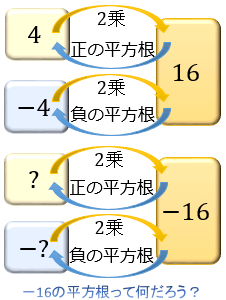おとな数学塾 Home Facebook
おとな数学塾 Home Facebook	おとな数学塾 Home Facebook	おとな数学塾 Home Facebook
おとな数学塾 Home Facebook	おとな数学塾 Home Facebook	おとな数学塾 Home Facebook
おとな数学塾 Home Facebook	おとな数学塾 Home Facebook	おとな数学塾 Home Facebook
おとな数学塾 Home Facebook	おとな数学塾 Home Facebook	おとな数学塾 Home Facebook
おとな数学塾 Home Facebook	おとな数学塾 Home Facebook	おとな数学塾 Home Facebook
おとな数学塾 Home Facebook	おとな数学塾 Home Facebook	おとな数学塾 Home Facebook
おとな数学塾 Home Facebook	おとな数学塾 Home Facebook	おとな数学塾 Home Facebook
おとな数学塾 Home Facebook	おとな数学塾 Home Facebook	おとな数学塾 Home Facebook
おとな数学塾 Home Facebook	おとな数学塾 Home Facebook	おとな数学塾 Home Facebook
おとな数学塾 Home Facebook	おとな数学塾 Home Facebook	おとな数学塾 Home Facebook
おとな数学塾 Home Facebook	おとな数学塾 Home Facebook	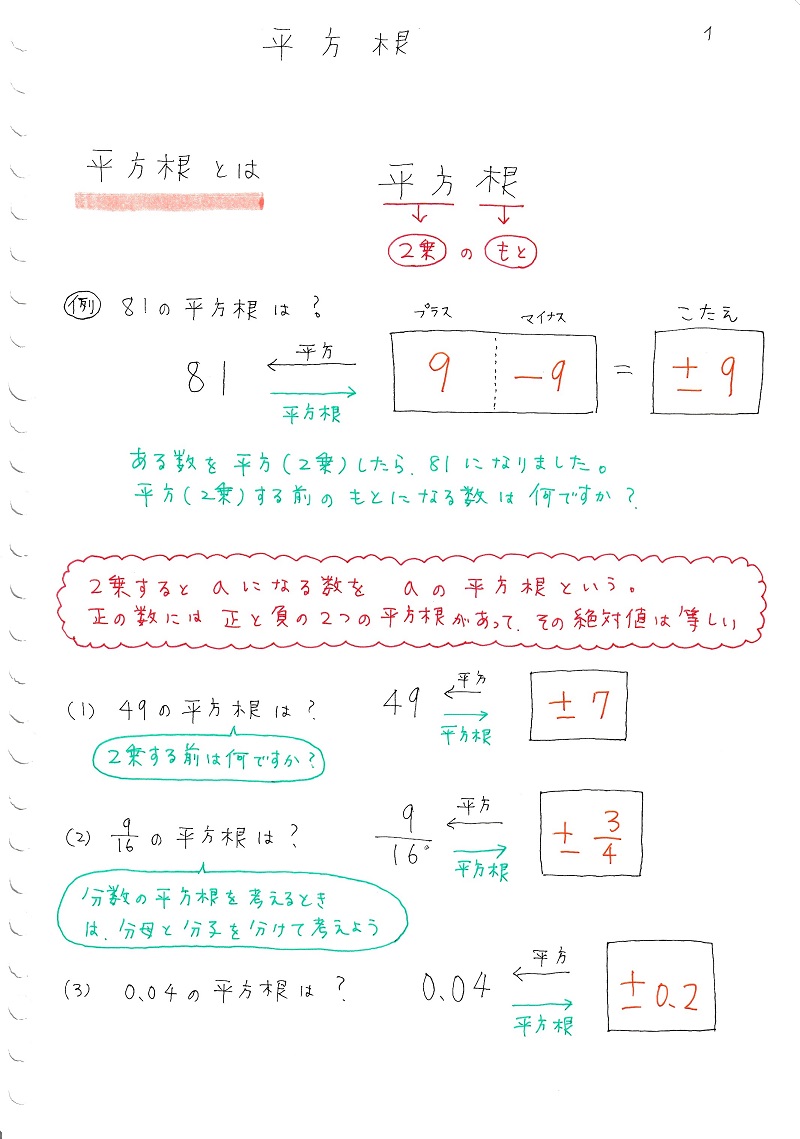おとな数学塾 Home Facebook
おとな数学塾 Home Facebook	おとな数学塾 Home Facebook	おとな数学塾 Home Facebook
おとな数学塾 Home Facebook	おとな数学塾 Home Facebook	おとな数学塾 Home Facebook
おとな数学塾 Home Facebook	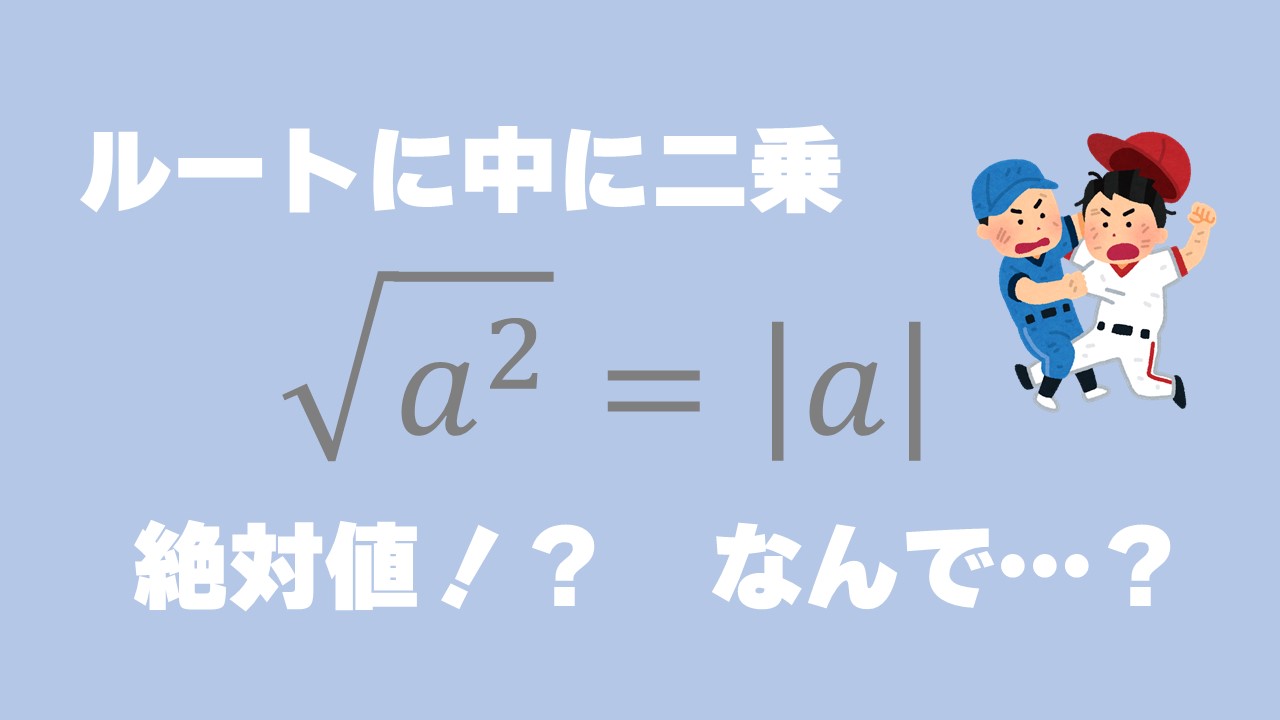おとな数学塾 Home Facebook	おとな数学塾 Home Facebook
おとな数学塾 Home Facebook	おとな数学塾 Home Facebook	おとな数学塾 Home Facebook
おとな数学塾 Home Facebook	おとな数学塾 Home Facebook	おとな数学塾 Home Facebook
おとな数学塾 Home Facebook	おとな数学塾 Home Facebook	おとな数学塾 Home Facebook
おとな数学塾 Home Facebook	おとな数学塾 Home Facebook	おとな数学塾 Home Facebook
おとな数学塾 Home Facebook	おとな数学塾 Home Facebook	おとな数学塾 Home Facebook
おとな数学塾 Home Facebook	おとな数学塾 Home Facebook	おとな数学塾 Home Facebook
おとな数学塾 Home Facebook	おとな数学塾 Home Facebook	おとな数学塾 Home Facebook
おとな数学塾 Home Facebook	おとな数学塾 Home Facebook	おとな数学塾 Home Facebook
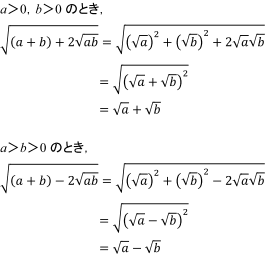おとな数学塾 Home Facebook	おとな数学塾 Home Facebook	おとな数学塾 Home Facebook
おとな数学塾 Home Facebook	おとな数学塾 Home Facebook	おとな数学塾 Home Facebook
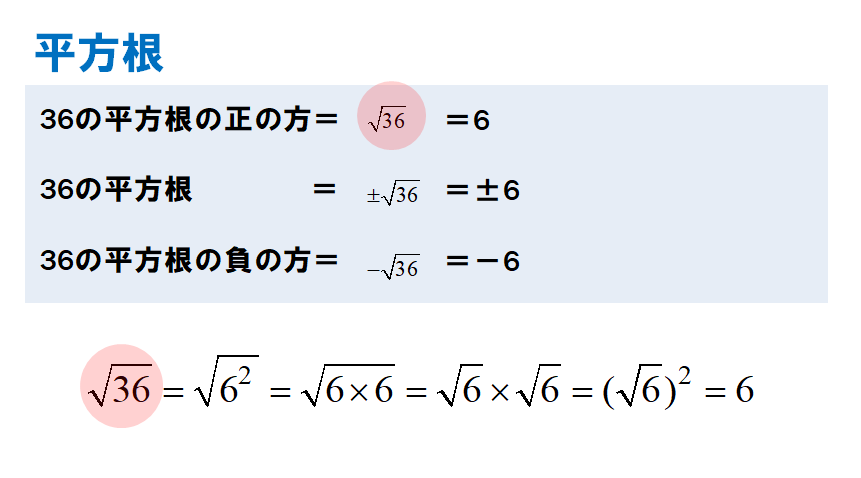おとな数学塾 Home Facebook	おとな数学塾 Home Facebook	おとな数学塾 Home Facebook
おとな数学塾 Home Facebook	おとな数学塾 Home Facebook	おとな数学塾 Home Facebook
おとな数学塾 Home Facebook	おとな数学塾 Home Facebook

 ・負の数の平方根の計算 負の数の平方根があるときは、$$~~~\sqrt{a}\times\sqrt{b}=\sqrt{ab}$$このような先にルートの中の計算をする公式は使えません。 よって、計算の順序は ① 負の数の平方根を \(i\) を用いて表す ② すべての平方根の中が正の数になったら、平方根の計算をする みなさんは『系統図』というものを知っていますか？ 系統図を意識すると、単元の繋がりが分かるのでより効率的に学習ができます。 本日は数と式、図形の分野で、繋がりが強い単元をいくつかご紹介させて頂きますね！ 結論 ① 正の数・負の数 ↓ 平方根

Incoming Term: 負の数の平方根 高校,